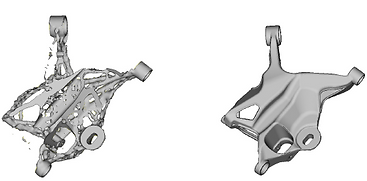
選択的レーザー溶融(SLM)
選択的レーザー溶融または金属粉末床融合は、熱源を使用して金属粉末粒子間の融合を一度に1層ずつ誘導し、固体オブジェクトを生成する3D印刷プロセスです。
ほとんどのPowderBed Fusionテクノロジーは、オブジェクトの構築時に粉末を追加するメカニズムを採用しているため、最終的なコンポーネントが金属粉末に包まれます。金属粉末床融合技術の主なバリエーションは、さまざまなエネルギー源の使用に由来します。レーザーまたは電子ビーム。
3D印刷技術の種類: 直接金属レーザー焼結(DMLS);選択的レーザー溶融(SLM);電子ビーム溶解(EBM)。
材料: 金属粉末:アルミニウム、ステンレス鋼、チタン。
寸法精度: ±0.1mm。
一般的なアプリケーション: 機能性金属部品(航空宇宙および自動車);医学;歯科。
強み: 最強の機能部品。複雑な形状。
弱点: 小さいビルドサイズ。すべてのテクノロジーの中で最も高い価格。
選択的レーザー溶融(SLM)
選択的レーザー溶融または金属粉末床融合は、熱源を使用して金属粉末粒子間の融合を一度に1層ずつ誘導し、固体オブジェクトを生成する3D印刷プロセスです。
ほとんどのPowderBed Fusionテクノロジーは、オブジェクトの構築時に粉末を追加するメカニズムを採用しているため、最終的なコンポーネントが金属粉末に包まれます。金属粉末床融合技術の主なバリエーションは、さまざまなエネルギー源の使用に由来します。レーザーまたは電子ビーム。
3D印刷技術の種類: 直接金属レーザー焼結(DMLS);選択的レーザー溶融(SLM);電子ビーム溶解(EBM)。
材料: 金属粉末:アルミニウム、ステンレス鋼、チタン。
寸法精度: ±0.1mm。
一般的なアプリケーション: 機能性金属部品(航空宇宙および自動車);医学;歯科。
強み: 最強の機能部品。複雑な形状。
弱点: 小さいビルドサイズ。すべてのテクノロジーの中で最も高い価格。
選択的レーザー溶融(SLM)
選択的レーザー溶融または金属粉末床融合は、熱源を使用して金属粉末粒子間の融合を一度に1層ずつ誘導し、固体オブジェクトを生成する3D印刷プロセスです。
ほとんどのPowderBed Fusionテクノロジーは、オブジェクトの構築時に粉末を追加するメカニズムを採用しているため、最終的なコンポーネントが金属粉末に包まれます。金属粉末床融合技術の主なバリエーションは、さまざまなエネルギー源の使用に由来します。レーザーまたは電子ビーム。
3D印刷技術の種類: 直接金属レーザー焼結(DMLS);選択的レーザー溶融(SLM);電子ビーム溶解(EBM)。
材料: 金属粉末:アルミニウム、ステンレス鋼、チタン。
寸法精度: ±0.1mm。
一般的なアプリケーション: 機能性金属部品(航空宇宙および自動車);医学;歯科。
強み: 最強の機能部品。複雑な形状。
弱点: 小さいビルドサイズ。すべてのテクノロジーの中で最も高い価格。
構造最適化
進化するCAE(コンピューター支援エンジニアリング)および製造技術は、従来の設計パラダイムに取って代わりました。シミュレーションと分析への移行により、さまざまな設計と製造の目標を達成することができました。トポロジー最適化、形状最適化、パラメトリック最適化、設計空間探索などのさまざまなCAE手法が、現在、構造最適化に使用されています。
構造最適化によって達成できる設計目標は次のとおりです。
軽量設計
地域全体のストレスの軽減
さまざまな境界条件への準拠。
コンポーネントの故障の削減
材料使用量の削減
構造設計の最適化は、大きく3つのカテゴリに分類できます。
1.サイズ:
典型的なサイジングの問題では、目標は線形弾性プレートの最適な厚さ分布またはトラス構造の最適な部材領域を見つけることかもしれません。
2.形状:
形状最適化は、すべての境界条件と荷重を満たしながら、局所領域全体の応力を低減するために行われます。最適化基準法を使用して、形状最適化を実現できます。このアルゴリズムは、領域全体で応力の均一性を維持し、構造の物理要素を変更して応力集中を低減しようとします。
3.トポロジーの最適化:
トポロジー最適化手法は、すべての境界条件と荷重制約を満たす、特定の設計空間での最適な材料分布を決定します。ペナルティのある固体等方性材料(SIMP)、進化的構造最適化(ESO)、双方向進化的構造最適化(BESO)など、さまざまな数学モデルがあります。最も一般的に使用される方法はSIMPであり、与えられた量の材料。剛性を使用する利点は、剛性をスカラー量として表すことができるため、計算効率が向上することです。